Solving Simultaneous Equations in Geometry
The task involves solving a pair of simultaneous equations to find the points of intersection between a line and a circle on a coordinate plane. It demonstrates the use of algebraic methods to determine the intersection points without graphing the functions. The process includes substitution and calculations to determine the values of variables. The solution is presented step by step, showcasing how mathematical concepts can help in geometric problem-solving.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
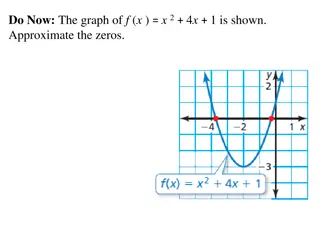
From last week ? Solve ? = 2? and ? = 4? + 7 using substitution ? From last month ? Write down the value of sin60 without using a calculator From last year Solve ?2+ ? 12 = 0
From last week 2? = 4? + 7 -2? = 7 Solve ? = 2? and ? = 4? + 7 using substitution ? = 3.5 ? = 7 From last month 3 Write down the value of sin60 without using a calculator 2 From last year Solve ?2+ ? 12 = 0 ? + 4 ? 3 = 0 ? = 4,? = 3
Use your axes to work out where the line given by the equation ? = ? + 1 intersects the circle ?2+ ?2= 25
The line ? = ? + 1 intersects the circle twice as shown. (3,4) How could we have worked out these points of intersection without sketching the graphs? ( 4,3)
Solving this pair of simultaneous equations will gives us the points of intersection. ?2+ ?2= 25 ? = ? + 1
Solving this pair of simultaneous equations will gives us the points of intersection. ?2+ ?2= 25 ? = ? + 1 Substituting for y gives: ?2+ (? + 1)2= 25 ?2+ ?2+ 2? + 1 = 25 2?2+ 2? 24 = 0 ?2+ ? 12 = 0 ? + 4 ? 3 = 0 ? = 4,? = 3
Solving this pair of simultaneous equations will gives us the points of intersection. ?2+ ?2= 25 ? = ? + 1 Using the equation of the straight line to calculate y: ? = 4,? = 3 ? = 3,? = 4
Use your axes to approximate where the line given by the equation ? = ? + 1 intersects the circle ?2+ ?2= 5
Use algebra to find where the line given by the equation ? = ? + 1 intersects the circle ?2+ ?2= 5
Title Intersections of curves and lines Worked Example Your Turn Calculate where the line Calculate where the line ? = 10 2? ? = 2? 10 intersects the circle described by equation ?2+ ?2= 20 intersects the circle described by equation ?2+ ?2= 40
In your book: 1. Work out the points of intersection of the circle ?2+ ?2= 58 and the line ? = 4 + ? 2. Work out the points of intersection of the curve ? + 5 = 3?2 14? and the line ? = 4? 32 3. Work out the points of intersection of the circle ?2+ ?2= 2 and the line ? = 2 3? 4. Work out the points of intersection of the curve 2?2 ?2+ ?? = 14 and the line 4? + 5? = 0
Mark your work 1. 7, 3 ??? 3,7 2. 3,20 3. 1,1 ??? 1.4,0.2 1,2 ??? (0. 1,2. 4) 4.
Challenge Overturning Fracsum Solve the following systems of equations to find the values of ?, ? and ?.