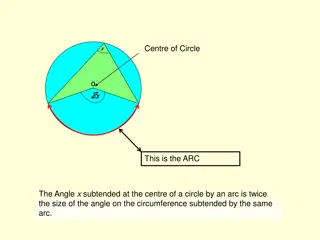
Trigonometry with Unit Circle Basics
Explore the fundamental concepts of trigonometry using the unit circle, including angles in standard position, quadrant analysis, and coordinate calculations. Gain insights into the coordinates of points on the unit circle and learn how to apply trigonometric functions to solve geometrical problems efficiently.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
10 July 2025 The first quadrant of the unit circle LO: Use the unit circle in trigonometry. www.mathssupport.org
Angles in standard position The angle in a Cartesian coordinate system has its vertex at the origin Initial side along the positive x axis So, it is said to be in Standard position The angle is measured from the x axis If the angle is anticlockwise it is said to be positive. Terminal side y y y x x x vertex 0 0 0 Initial side www.mathssupport.org www.mathssupport.org
Angles in standard position If we draw a circle with radius = 1 in a Cartesian coordinate system. The centre of the circle is at the origin, The radius is one unit. The angle is positive. This is called a unit circle. Now take a look at acute angle in the first quadrant of the unit circle. y B 1 1 A 0 x www.mathssupport.org www.mathssupport.org
The unit quarter circle y Now look at what happens when the line intersects the unit circle at the point P in the first quadrant. The line forms an angle with the x axis P (x y) 0 x www.mathssupport.org
The unit quarter circle Now look at what happens when the line intersects the unit circle y at the point P in the first quadrant. If we draw a line, perpendicular from P to the x axis A right angled triangle is formed OQP P (x y) Q 0 x www.mathssupport.org
The unit quarter circle Hypothenuse OP = 1. Adjacent side OQ = x Opposite side PQ = y sin =?? ?? = sin = y y ? 1 P (cos sin ) (x y) ? 1 cos =?? = ?? cos = x (x, y) = (cos , sin ) 1 =? ?=sin? cos? = sin y tan =?? ?? Using Pythagoras theorem = cos Q x cos2 + sin2 = 1 x www.mathssupport.org
The unit quarter circle (a) State exactly the coordinates of the point P. (b) Find the coordinates of P correct to 2 dp y (a) The coordinates of the point P:(cos o sin30o) P (b) The coordinates of the point P: ( ) 0.5 x www.mathssupport.org
Angles in standard position (a) State exactly the coordinates of the point P. (b) Find the coordinates of P correct to 3 sf (a) The coordinates of the point P: (cos o sin55o) y P (b) The coordinates of the point P: ( 0.819) 0 x www.mathssupport.org
Angles in standard position (a) State exactly the coordinates of the point Q. (b) Find the coordinates of Q correct to 3 sf (a) The coordinates of the point Q: (cos o sin166o) y Q (b) The coordinates of the point Q: ( 0.242) 0 x www.mathssupport.org
Angles in standard position (a) State exactly the coordinates of the point R. (b) Find the coordinates of R correct to 3 sf (a) The coordinates of the point R: (cos o sin247o) y (b) The coordinates of the point R: ( 0.921) 0 x R www.mathssupport.org
Angles in standard position (a) State exactly the coordinates of the point S. (b) Find the coordinates of S correct to 3 sf (a) The coordinates of the point S: (cos o sin311o) y (b) The coordinates of the point S: ( 0.755) 0 x S www.mathssupport.org
Angles in standard position (a) State exactly the coordinates of the point P. (cos o sin38o) (b) Find the coordinates of P correct to 3 sf ( 0.616) (c) State exactly the coordinates of the point Q. (cos o sin55o) (d) Find the coordinates of Q correct to 3 sf ( 0.616) What do you notice about the angles? y P Q cos = cos = What do you find about the cosine? 0 x In general we can say that: cos ( ) = cos sin ( ) = sin www.mathssupport.org
Thank you for using resources from A close up of a cage Description automatically generated For more resources visit our website https://www.mathssupport.org If you have a special request, drop us an email info@mathssupport.org www.mathssupport.org