Understanding Averages Through Examples
Explore the concept of averages through practical examples like calculating mean, median, and mode based on given data sets. Learn how to work with frequency tables to determine averages effectively. Enhance your understanding of statistical measures.
Uploaded on | 1 Views
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
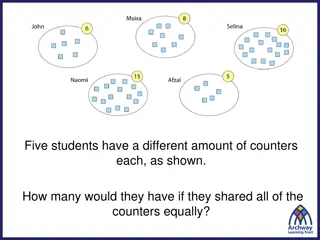
Starter Complete the jigsaw on averages. Remember: Mode is most Median is middle Mean is mean to work out Range is biggest - smallest
Averages from a Table Arsenal scored the following number of goals in their first 20 matches in the 2012/2013 Premier League season: 0, 0, 2, 6, 1, 3, 0, 1, 1, 3, 5, 0, 1, 0, 2, 5, 1, 7, 1, 0 http://news.bbcimg.co.uk/media/images/64857000/jpg/_64857018_arsenal_five_players_getty.jpg Work out the mean using the Frequency Table.
Averages from a Table Goals 0 1 2 3 4 5 6 7 Total Freq. 6 6 2 2 0 2 1 1 20 First put the data into a frequency table. In this case there are two modes the data is bimodal. We can clearly see that the modes were no goals and one goal.
Averages from a Table Goals 0 1 2 3 4 5 6 7 Total Freq. 6 6 2 2 0 2 1 1 20 Altogether there were 20 goals. 6 12 To calculate the location of the median: 20 + 1 = 10.5th piece of data 2 The median lies in the second box, so is 1 goal.
Averages from a Table To calculate the mean: Goals 0 1 2 3 4 5 6 7 Total Freq. 6 6 2 2 0 2 1 1 20 m x f 0 6 4 6 0 10 6 7 39 There are 6 0s, 6 1s, 2 2s, etc, so we can multiply across to make adding quicker! Then calculate the total and divide by the number of goals. 39 20 = 1.95 goals
Averages from a Table Maria has 45 pairs of shoes and recorded how much each pair costs. Price 0 < 10 10 < 20 20 < 30 30 < 40 40 < 50 50 < 100 100 < 150 150 < 200 Total Freq. 3 6 2 12 13 6 2 1 45 The modal class is 40 < 50 as it has the highest frequency.
Averages from a Table Price 0 < 10 10 < 20 20 < 30 30 < 40 40 < 50 50 < 100 100 < 150 150 < 200 Total Freq. 3 6 2 12 13 6 2 1 45 The median: 3 9 11 23 45 + 1 = 23rd pair of shoes 2 The class in which the median lies is 30 < 40.
Averages from a Table Can we calculate the mean? As we do not know the exact value of each piece of data, we can only calculate an estimate for the mean. We cannot multiply by a class interval, so we need to choose an appropriate number from each group to multiply by the frequency. What should we choose? The midpoint
Averages from a Table Price 0 < 10 10 < 20 20 < 30 30 < 40 40 < 50 50 < 100 100 < 150 150 < 200 Total Freq. 3 6 2 12 13 6 2 1 45 Mid. 5 15 25 35 m x f 15 90 50 Estimate for the mean 2035 45 = 37 420 585 450 45 75 125 250 175 2035 175
Answers Mean Mode Median Q1 5.55 5 5 Q2 2.73 1 3 Q3 11.67 9 < x 12 9 < x 12 Q4 3.09 3 - 4 3 4 Q5 60.75 60 < t 70 60 < t 70