Laplace Interpolation for Sparse Data Restoration
Laplace Interpolation is a method used in CSE 5400 by Joy Moore for interpolating sparse data points. It involves concepts such as the mean value property, handling boundary conditions, and using the A-times method. The process replaces missing data points with a designated value and approximates in
7 views • 13 slides
Noise Sensitivity in Sparse Random Matrix's Top Eigenvector Analysis
Understanding the noise sensitivity of the top eigenvector in sparse random matrices through resampling procedures, exploring the threshold phenomenon and related works. Results highlight the impact of noise on the eigenvector's stability and reliability in statistical analysis.
4 views • 7 slides
Sparse vs. Dense Vector Representations in Natural Language Processing
Tf-idf and PPMI are sparse representations, while alternative dense vectors offer shorter lengths with non-zero elements. Dense vectors may generalize better and capture synonymy effectively compared to sparse ones. Learn about dense embeddings like Word2vec, Fasttext, and Glove, which provide effic
1 views • 44 slides
Overview of Sparse Linear Solvers and Gaussian Elimination
Exploring Sparse Linear Solvers and Gaussian Elimination methods in solving systems of linear equations, emphasizing strategies, numerical stability considerations, and the unique approach of Sparse Gaussian Elimination. Topics include iterative and direct methods, factorization, matrix-vector multi
1 views • 35 slides
Dynamic Load Balancing in Block-Sparse Tensor Contractions
This paper discusses load balancing algorithms for block-sparse tensor contractions, focusing on dynamic load balancing challenges and implementation strategies. It explores the use of Global Arrays (GA), performance experiments, Inspector/Executor design, and dynamic buckets implementation to optim
3 views • 32 slides
Threaded Construction and Fill of Tpetra Sparse Linear System Using Kokkos
Tpetra, a parallel sparse linear algebra library, provides advantages like solving problems with over 2 billion unknowns and performance portability. The fill process in Tpetra was not thread-scalable, but it is being addressed using the Kokkos programming model. By utilizing Kokkos data structures
2 views • 19 slides
Statistical Dependencies in Sparse Representations: Exploitation & Applications
Explore how to exploit statistical dependencies in sparse representations through joint work by Michael Elad, Tomer Faktor, and Yonina Eldar. The research delves into practical pursuit algorithms using the Boltzmann Machine, highlighting motivations, basics, and practical steps for adaptive recovery
0 views • 47 slides
Efficient Coherence Tracking in Many-core Systems Using Sparse Directories
This research focuses on utilizing tiny, sparse directories for efficient coherence tracking in many-core systems. By optimizing directory entries and leveraging sharing patterns, the proposed approach achieves high performance with minimal on-chip area investment. Results demonstrate significant en
5 views • 66 slides
Communication Costs in Distributed Sparse Tensor Factorization on Multi-GPU Systems
This research paper presented an evaluation of communication costs for distributed sparse tensor factorization on multi-GPU systems. It discussed the background of tensors, tensor factorization methods like CP-ALS, and communication requirements in RefacTo. The motivation highlighted the dominance o
4 views • 34 slides
Batch Estimation and Solving Sparse Linear Systems
Explore the concepts of batch estimation, solving sparse linear systems, and Square Root Filters in the context of information and square-root form. Learn about extended information filters, information filter motion updates, measurement updates, factor graph optimization, and more. Understand how S
4 views • 37 slides
Efficient Hardware Architectures for Deep Neural Network Processing
Discover new hardware architectures designed for efficient deep neural network processing, including SCNN accelerators for compressed-sparse Convolutional Neural Networks. Learn about convolution operations, memory size versus access energy, dataflow decisions for reuse, and Planar Tiled-Input Stati
4 views • 23 slides
Orthogonal Vectors Conjecture and Sparse Graph Properties Workshop
Exploring the computational complexity of low-polynomial-time problems, this workshop delves into the Orthogonal Vectors Problem and its conjectures. It introduces concepts like the Sparse OV Problem, first-order graph properties, and model checking in graphs. Discussing the hardness of problems rel
7 views • 22 slides
Sparse-TPU: Adapting Systolic Arrays for Sparse Matrices
This paper explores Sparse-TPU, a novel approach that modifies systolic arrays to efficiently handle sparse matrix workloads, achieving significant speedup and energy savings compared to traditional TPUs. The content delves into matrix packing, dataflow, PE design, and algorithm optimization within
0 views • 27 slides
Sparse Matrix-Vector Multiply on Keystone II DSP
Sparse matrix-vector multiplication on the Keystone II Digital Signal Processor (DSP) is explored in this research presented at the IEEE High Performance Extreme Computing Conference. The study delves into the hardware features of the Keystone II platform, including its VLIW processor architecture a
1 views • 20 slides
Performance of Supervised and Semi-Supervised Methods for Sparse Matrix Selection
This paper discusses the performance of supervised and semi-supervised methods for automated sparse matrix format selection in the context of accelerators. The study was presented at the International Workshop on Deployment and Use of Accelerators. The authors compare and analyze the effectiveness o
3 views • 23 slides
ExTensor: An Accelerator for Sparse Tensor Algebra
Cutting-edge accelerator designed for sparse tensor algebra operations. It introduces hierarchical intersection architecture for efficient handling of sparse tensor kernels, unlocking potential in diverse domains like deep learning, computational chemistry, and more.
3 views • 23 slides
HTS: A Multithreaded Direct Sparse Triangular Solver
This article discusses a multithreaded direct sparse triangular solver that combines level scheduling and recursive blocking techniques. The problem statement, solution approach, algorithms, and implementation details are covered, focusing on efficiency in handling sequential RHS with the same nonze
5 views • 18 slides
Sparse Matrix Algorithms: Permutations and Chordal Completion
Most coefficients in matrices are zero, leading to sparsity. Sparse Gaussian elimination and chordal completion aim to minimize edges while solving matrices efficiently. The 2D model problem illustrates behaviors of sparse matrix algorithms. Permutations impact fill levels, with natural and nested d
2 views • 29 slides
Enhancing Scientific Document Retrieval with Hybrid Approach
A hybrid approach combining sparse and dense retrieval methods to improve scientific document retrieval. Sparse models use high-dimensional Bag of Words vectors with TF-IDF weights, while dense models employ transformer-based LLM for nuanced vector representations. By leveraging both sparse and dens
4 views • 14 slides
Sparse Matrix Analysis for Drug Discovery Research
The pharmaceutical industry is grappling with rising costs and stagnant R&D productivity. To address this, research is focused on utilizing sparse matrix analysis of small molecules and protein targets. By applying innovative technology and cloud-based solutions, researchers aim to streamline drug d
4 views • 19 slides
Efficient and Effective Sparse LSTM on FPGA with Bank-Balanced Sparsity
Utilizing Bank-Balanced Sparsity, this work presents an efficient Sparse LSTM implementation on FPGA for real-time inference in various applications like machine translation, speech recognition, and synthesis. Through innovative design and evaluation, the model achieves high accuracy while maintaini
0 views • 52 slides
Sparse Matrix Reordering Interpretations
Sparse matrix reordering techniques such as Tinney Ordering Scheme and Permutation Vectors are discussed in this content. These methods help optimize the arrangement of nodes in electrical systems for efficient analysis. The associated graphs and mathematical concepts are explored, emphasizing the i
4 views • 28 slides
Communication Costs for Distributed Sparse Tensor Factorization on Multi-GPU Systems
Evaluate communication costs for distributed sparse tensor factorization on multi-GPU systems in the context of Supercomputing 2017. The research delves into background, motivation, experiments, results, discussions, conclusions, and future work, emphasizing factors like tensors, CP-ALS, MTTKRP, and
5 views • 34 slides
Sparse Linear Solvers: Strategies and Gaussian Elimination Overview
Explore the concepts of sparse linear solvers, including strategies for solving systems of linear equations with many zeros, the distinction between direct and iterative methods, and an overview of Gaussian Elimination for numerical stability. Gain insights into the algorithms, techniques, and consi
1 views • 35 slides
Origin and Pursuit of the Analysis Co-Sparse Model
Explore the development and significance of the analysis (co-)sparse model in signal modeling, highlighting its distinction from the synthesis model. Learn about the potential of this approach for dictionary learning and beyond.
2 views • 29 slides
Sparse Models Analysis Using K-SVD Dictionary Learning
Explore K-SVD dictionary learning for analysis of sparse models, covering synthesis representation, pursuit algorithms, dictionary learning, and the K-SVD model. Understand the basics, strategies for sparse coding, and the dictionary update process to enhance signal recovery.
1 views • 29 slides
Dynamic Sparse Channel Reconstruction through Matching Pursuit
Learn about the Structured Matching Pursuit method for reconstructing dynamic sparse channels efficiently utilizing compressive sensing algorithms such as Orthogonal Matching Pursuit (OMP) and Compressive Sampling Matching Pursuit (CoSaMP). Explore the system model, temporal correlation of dynamic c
0 views • 14 slides
Dynamic Sparse Channel Tracking Using Differential Detection
Explore the innovative approach of utilizing compressive sensing for dynamic sparse channel recovery using differential detection, reducing training overhead while maintaining spectrum efficiency. Learn about various algorithms such as Orthogonal Matching Pursuit (OMP) and the advantages of exploiti
0 views • 12 slides
Compressed Sensing Algorithms for Big Data Lecture
Learn about Compressed Sensing, a technique to recover sparse signals from a small number of measurements, its applications in signal processing, reconstruction methods, subgradient optimization, exact reconstruction properties, and the restricted isometry property of matrices. Explore how Compresse
3 views • 11 slides
Resolving Space-Hard Function Challenges through Sparse Polynomial Techniques
Discover how sparse polynomials are utilized to address issues related to space-hard functions in various cryptographic scenarios such as Space-Lock Puzzles, Verifiable Delay Functions (VDFs), and Permutation Polynomials. Learn about techniques for resolving space-hardness problems, verifiable compu
2 views • 11 slides
Sparse Matrix Operations and Graph Partitioning
Explore the concepts of sparse matrix-vector multiplication, graph partitioning, and their applications in parallel computing. Learn about strategies to optimize communication volume and reduce edge crossings, as well as common applications such as solving equations and data mining.
0 views • 37 slides
Sparse Linear Solvers: Strategies and Methods
Explore sparse linear solvers, including direct and iterative methods like Gaussian elimination and Sparse GE, along with numerical stability considerations like pivoting. Learn how to solve systems of linear equations efficiently in a sparse matrix setting.
1 views • 35 slides
Sparse Model Analysis in Dictionary Learning with Michael Elad
Explore the principles of dictionary learning for analysis sparse models presented by Michael Elad, highlighting the background of synthesis and analysis models, Bayesian perspectives, and the concept of Union-of-Subspaces for generating analysis signals. Discover the basics of the synthesis and ana
3 views • 23 slides
Sparse Matrix-Vector Multiply on Texas Instruments C6678 DSP
Explore the unique architectural features of Texas Instruments C6678 Digital Signal Processor and its efficiency compared to competing coprocessors like NVIDIA Tesla K20X GPU and Intel Xeon Phi 5110p. Learn about software pipelining, sparse matrices evaluation, and code implementation for matrix-vec
2 views • 24 slides
Sparse LU Factorization in Electrical Systems Analysis
Exploit the structure of sparse matrices for efficient LU factorization in analyzing large-scale electrical systems. Compare sparse direct solution methods with iterative methods for solving linear systems. Learn about the history of sparse matrices and their development in various disciplines since
2 views • 47 slides
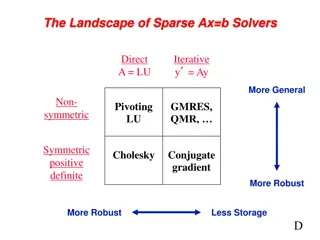
Sparse Ax=b Solvers and Cholesky Factorization
Discover the landscape of sparse Ax=b solvers, from direct solvers like LU to iterative methods such as GMRES and QMR. Explore Cholesky factorization techniques, including both general and sparse column approaches. Learn about sparse Gaussian elimination, Chordal completion, and the Cholesky graph g
3 views • 21 slides
Enhancing Scientific Document Retrieval with Hybrid Approach
A comparison of sparse and dense information retrieval methods in the academic domain, highlighting the strengths and weaknesses of traditional sparse encoding, deep-learning based dense retrieval, and the effectiveness of a hybrid approach. The study showcases how combining sparse and dense vector
0 views • 14 slides
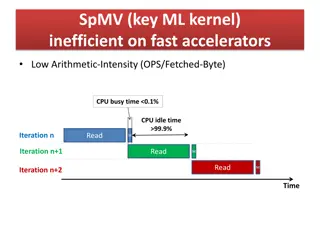
Efficient Sparse Matrix-Vector Multiplication on Accelerators
Implementing an efficient SpMV kernel on fast accelerators with low arithmetic intensity can be challenging. This content discusses common and new solutions utilizing space-efficient formats like Compressed Sparse Row (CSR) and variations (CSR-DU/VI) to achieve higher operational intensity and perfo
6 views • 4 slides
Learn OpenMP for Sparse Matrix-Vector Operations | CMU 15-418/15-618
Join CMU's 15-418/15-618 to master OpenMP programming for sparse matrix-vector operations. Enhance your understanding of CSR format and parallel computing strategies for irregular matrices. Explore code implementations and parallelism with OpenMP to optimize matrix-vector multiplication.
2 views • 48 slides
Analysis Techniques for Large-Scale Electrical Systems: Sparse Matrix Reordering and Permutation Vectors
Explore the utilization of permutation vectors and sparse matrix reordering in analyzing large-scale electrical systems. Learn how Tinney's scheme and graph theory play essential roles in this context.
0 views • 34 slides