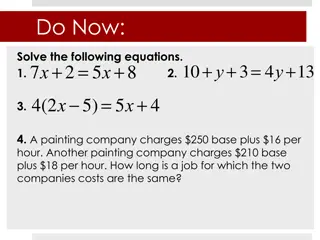Problem Solving with Simultaneous Equations - Step-by-Step Guide
Learn how to solve word problems using simultaneous equations with this comprehensive guide. Understand the steps involved in creating and solving equations to find solutions. Practice examples such as finding the cost of tickets or determining the sum and difference of numbers. Improve your problem-solving skills in mathematics with clear explanations and practical examples.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
13 April 2025 Problem solving using simultaneous equations LO: To create equations from word problems in order to solve them. www.mathssupport.org
Problem solving with simultaneous equations Many problems can be described using a pair of linear equations You should follow these steps: Step 1 : Decide on the two unknowns, for example x and y. Do not forget the units. Step 2 : Write down two equations connecting x and y. Step 3 : Solve the equations simultaneously. Step 4 : Check that your solution satisfies the original problem. Step 5 : Write your answer in sentence form. www.mathssupport.org www.mathssupport.org
Constructing an equation Example 1 Two adult s tickets and three children s tickets to a football match cost 45. Three adult s and four children's tickets cost 64. Find the cost of each type of ticket Step 1 : Decide on the two unknowns, for example x and y. Do not forget the units. Let xbe the cost of an adult s ticket Let ybe the cost of a child s ticket Step 2 : Write down two equations connecting x and y. 2x 3x 45 64 3y 4y = = + + Use the GDC Step 3 : Solve the equations simultaneously. x 12 = 7 = y Check in 2 Step 4 : Check that your solution satisfies the original problem. 3 4 + (12) (7) Step 5 : Write your answer in sentence form. An adult s ticket cost 12. A child s ticket cost 7 64 36 = + 28 = www.mathssupport.org
Solving problems The sum of two numbers is 56 and the difference between the two numbers is 22. Find the two numbers. Solving problems Step 1 : Decide on the two unknowns, for example a and b. Let s call the unknown numbers aandb. Step 2 : Write down two equations connecting a and b. We can use the given information to write a pair of simultaneous equations in terms of aandb, The sum of a and b is 56 The difference between a and b is 22 Step 3 : Solve the equations simultaneously. a + b = 56 a b = 22 Use the GDC b = 17 a = 39 Check in 2 Step 4 : Check that your solution satisfies the original problem. 39 17 = 22 Step 5 : Write your answer in sentence form. The two numbers are 39 and 17. www.mathssupport.org
Solving problems Two numbers have a difference of 7 and an average of 4. Find the two numbers. Step 1 : Decide on the two unknowns, for example x and y. Let s call the unknown numbers xandy. Step 2 : Write down two equations connecting x and y. We can use the given information to write a pair of simultaneous equations in terms of xandy, The difference between x and y is: The average of x and y is: x y = 7 1 2? +1 2? = 4 ?+? 2 = 4 Step 3 : Solve the equations simultaneously. Use the GDC y= 0.5 x = 7.5 Step 4 : Check that your solution satisfies the original problem. 7.5 0.5 = 7 Step 5 : Write your answer in sentence form. The two numbers are 7.5 and 0.5. www.mathssupport.org
Solving problems The cost of theatre tickets for 4 adults and 3 children is 47.50. The cost for 2 adults and 6 children is 44. How much does each adult and child ticket cost? Step 1 : Decide on the two unknowns. Let s call the cost of an adult s ticket a and the cost of a child s ticket c. Step 2 : Write down two equations connecting x and y. 4a + 3c= 47.50 2a + 6c= 44 Use the GDC c= 4.50 4 adults and 3 children cost $47.50, so: 2 adults and 6 children cost $44, so: Step 3 : Solve the equations simultaneously. a= 8.50 Step 4 : Check that your solution satisfies the original problem. 4(8.50) + 3(4.50) = 47.50 Step 5 : Write your answer in sentence form. The cost of an adult s ticket is 8.50, and the cost of a child s ticket is 4.50. www.mathssupport.org
Thank you for using resources from A close up of a cage Description automatically generated For more resources visit our website https://www.mathssupport.org If you have a special request, drop us an email info@mathssupport.org www.mathssupport.org