Understanding Markov Chains in System Modeling
Explore the basics of Markov chains, terminology, properties, and analysis in system modeling. Learn about irreducibility, ergodicity, stationarity, and more. Dive into examples like the On-Off traffic model and TCP congestion window evolution.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Markov Chains Carey Williamson Department of Computer Science University of Calgary Winter 2018
2 Outline Plan: Introduce basics of Markov models Define terminology for Markov chains Discuss properties of Markov chains Show examples of Markov chain analysis On-Off traffic model Markov-Modulated Poisson Process Erlang B blocking formula TCP congestion window evolution
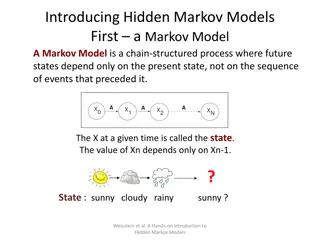
3 Definition: Markov Chain A discrete-state Markov process Has a set S of discrete states: |S| > 1 Changes randomly between states in a sequence of discrete steps Continuous-time process, although the states are discrete Very general modeling technique used for system state, occupancy, traffic, queues, ... Analogy: Finite State Machine (FSM) in CS
4 Some Terminology (1 of 3) Markov property: behaviour of a Markov process depends only on what state it is in, and not on its past history (i.e., how it got there, or when) A manifestation of the memoryless property, from the underlying assumption of exponential distributions
5 Some Terminology (2 of 3) The time spent in a given state on a given visit is called the sojourn time Sojourn times are exponentially distributed and independent Each state i has a parameter q_i that characterizes its sojourn behaviour
6 Some Terminology (3 of 3) The probability of changing from state i to state j is denoted by p_ij This is called the transition probability (sometimes called transition rate) Often expressed in matrix format Important parameters that characterize the system behaviour
7 Desirable Properties of Markov Chains Irreducibility: every state is reachable from every other state (i.e., there are no useless, redundant, or dead-end states) Ergodicity: a Markov chain is ergodic if it is irreducible, aperiodic, and positive recurrent (i.e., can eventually return to a given state within finite time, and there are different path lengths for doing so) Stationarity: stable behaviour over time
8 Analysis of Markov Chains The analysis of Markov chains focuses on steady-state behaviour of the system Called equilibrium, or long-run behaviour as time t approaches infinity Well-defined state probabilities p_i (non- negative, normalized, exclusive) Flow balance equations can be applied
9 Examples of Markov Chains Traffic modeling: On-Off process Interrupted Poisson Process (IPP) Markov-Modulated Poisson Process Computer repair models (server farm) Erlang B blocking formula Birth-Death processes M/M/1 Queueing Analysis